이코테 정확한 순위 Python
❍ 문제
선생님은 시험을 본 학생 N명의 성적을 분실하고, 성적을 비교한 결과의 일부만 가지고 있습니다.
학생 N명의 성적은 모두 다른데, 다음은 6명의 학생에 대하여 6번만 성적을 비교한 결과입니다.
- 1번 학생의 성적 < 5번 학생의 성적
- 3번 학생의 성적 < 4번 학생의 성적
- 4번 학생의 성적 < 2번 학생의 성적
- 4번 학생의 성적 < 6번 학생의 성적
- 5번 학생의 성적 < 2번 학생의 성적
- 5번 학생의 성적 < 4번 학생의 성적
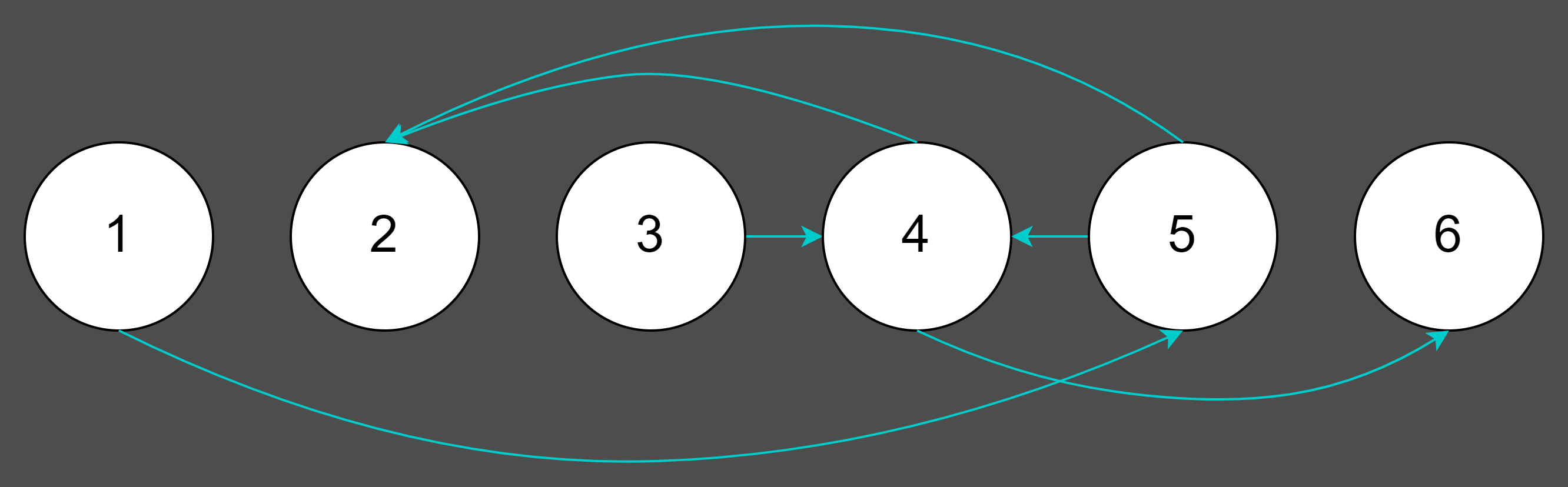
A번 학생의 성적이 B번 학생보다 낮다면 화살표가 A에서 B를 가리키도록 할 때 위의 성적 결과를 다음 그림처럼 표현할 수 있습니다.

이 그림으로 유추해서 순위를 정확히 알 수 있는 학생도 있고, 알 수 없는 학생도 있습니다. 예를 들어 1번 학생은 5번 학생보다 성적이 낮고, 5번 학생은 4번 학생보다 성적이 낮으므로 1번 학생은 4번 학생보다 성적이 낮습니다. 따라서 1번, 3번, 5번 학생은 모두 4번 학생보다 성적이 낮다고 볼 수 있습니다. 그리고 4번 학생은 2번 학생과 6번 학생보다 성적이 낮습니다. 정리하면 4번 학생보다 성적이 낮은 학생은 3명이고, 성적이 높은 학생은 2명이므로 4번 학생의 성적 순위를 정확히 알 수 있습니다. 하지만 예시에서 4번 학생을 제외한 다른 학생은 정확한 순위를 알 수 없습니다.
학생들의 성적을 비교한 결과가 주어질 때, 성적 순위를 정확히 알 수 있는 학생은 모두 몇 명인지 계산하는 프로그램을 작성하세요.
❍ 입력
- 첫째 줄에 학생들의 수 N(2 <= n <= 500)과 두 학생의 성적을 비교한 횟수 M(2 <= M <= 10,000)이 주어집니다.
- 다음 M개의 각 줄에는 두 학생의 성적을 비교한 결과를 나타내는 두 양의 정수 A와 B가 주어집니다.이는 A번 학생의 성적이 B번 학생보다 낮다는 것을 의미합니다.
❍ 출력
첫째 줄에 성적 순위를 정확히 알 수 있는 학생이 몇 명인지 출력합니다.
❏ 문제 풀이
각 학생들의 정확한 순위를 알기 위해선, 해당 노드가 다른 모든 노드들로 도달할 수 있어야 한다.
따라서, 플로이드 워셜 알고리즘을 이용하여, 모든 노드에서 모든 노드로 향하는 최단 경로를 계산하고, 반드시 다른 노드로 향하는 경로가 모두 있는 학생만을 세어준다.
❍ Code
import sys
input = sys.stdin.readline
n, m = map(int, input().split())
INF = int(1e9)
graph = [[INF] * (n + 1) for _ in range(n + 1)]
for i in range(n + 1):
for j in range(n + 1):
if i == j:
graph[i][j] = 0
break
for _ in range(m):
a, b = map(int, input().split())
graph[a][b] = 1
for k in range(1, n + 1):
for a in range(1, n + 1):
for b in range(1, n + 1):
graph[a][b] = min(graph[a][b], graph[a][k] + graph[k][b])
result = 0
for i in range(1, n + 1):
count = 1
for j in range(1, n + 1):
if graph[i][j] != INF or graph[j][i] != INF:
count += 1
if count == n:
result += 1
print(result)
❍ 시간 복잡도
시간 복잡도는 $O(N^3)$ 이다.