[BOJ/Python] 점프 || 다이나믹 프로그래밍

백준 점프 파이썬 1890

1890번: 점프

❏ 문제 설명

❍ 문제

N×N 게임판에 수가 적혀져 있다. 이 게임의 목표는 가장 왼쪽 위 칸에서 가장 오른쪽 아래 칸으로 규칙에 맞게 점프를 해서 가는 것이다.

각 칸에 적혀있는 수는 현재 칸에서 갈 수 있는 거리를 의미한다. 반드시 오른쪽이나 아래쪽으로만 이동해야 한다. 0은 더 이상 진행을 막는 종착점이며, 항상 현재 칸에 적혀있는 수만큼 오른쪽이나 아래로 가야 한다. 한 번 점프를 할 때, 방향을 바꾸면 안 된다. 즉, 한 칸에서 오른쪽으로 점프를 하거나, 아래로 점프를 하는 두 경우만 존재한다.

가장 왼쪽 위 칸에서 가장 오른쪽 아래 칸으로 규칙에 맞게 이동할 수 있는 경로의 개수를 구하는 프로그램을 작성하시오.

❍ 입력

첫째 줄에 게임 판의 크기 N (4 ≤ N ≤ 100)이 주어진다. 그 다음 N개 줄에는 각 칸에 적혀져 있는 수가 N개씩 주어진다. 칸에 적혀있는 수는 0보다 크거나 같고, 9보다 작거나 같은 정수이며, 가장 오른쪽 아래 칸에는 항상 0이 주어진다.

❍ 출력

가장 왼쪽 위 칸에서 가장 오른쪽 아래 칸으로 문제의 규칙에 맞게 갈 수 있는 경로의 개수를 출력한다. 경로의 개수는 263-1보다 작거나 같다.

 

❏ 문제 풀이

❍ 풀이

경로의 개수를 모두 구해주면, 시간 초과로 해당 문제를 풀어줄 수 없다. 다이나믹 프로그래밍은 똑같은 문제는 연산이 진행되지 않는다는 특징이 있는데, 이 문제의 경우, 시작점으로부터 해당 칸까지의 경로의 수를 누적하며 최종 결과를 얻을 수 있기에, 시간이 더 적게 걸린다.
(0, 0)인 시작점으로부터 가장 끝 칸인 (n - 1, n - 1)까지의 경로의 개수를 dp 리스트에 담아가며 문제를 해결하면 된다.
바텀업 방식 즉, 반복문을 이용하여 풀이를 해주었으며, dp 리스트를 생성하여 메모이제이션을 적용시켜주었다.
 
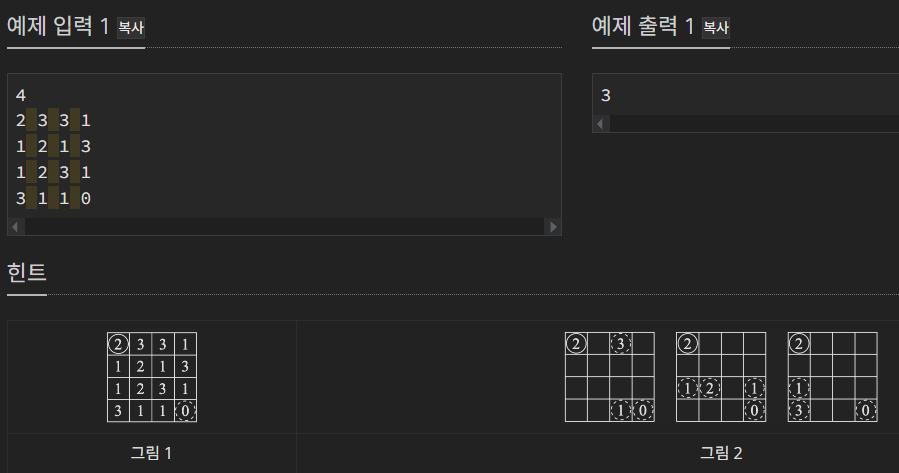
먼저, 시작점 (0, 0)의 규칙은 2이다. 따라서 (2, 0)과 (0, 2)까지 이동할 수 있는 경로가 확보된다. dp[i][j]로 2차원 배열을 이용하여 (i, j)까지의 이동 가능한 경로의 수를 의미하도록 하였다.
dp[0][2] = dp[0][0] + dp[0][2], dp[2][0] = dp[0][0] + dp[2][0]이 된다.
 
이를 코드로 표현하면 다음과 같다.
 

❍ CODE

import sys

input = sys.stdin.readline

n = int(input())
arr = [list(map(int, input().split())) for _ in range(n)]

dp = [[0 for _ in range(n)] for _ in range(n)]

dp[0][0] = 1

for i in range(n):
    for j in range(n):
        if i == n -1 and j == n - 1:
            break
        cnt = arr[i][j]

        if i + cnt < n:
            dp[i + cnt][j] += dp[i][j]
        
        if j + cnt < n:
            dp[i][j + cnt] += dp[i][j]

print(dp[n - 1][n - 1])

i가 n -1이고 j가 n -1일 경우 반복문을 종료한다. 종료하지 않으면, n을 넘지 않다보니, 해당 칸까지의 경로의 수가 중복으로 반영되게 된다.
cnt는 해당 칸의 규칙을 의미하여, cnt만큼 오른쪽과 아래로 이동하여 arr을 벗어나지 않는 경우, 해당 칸의 경로의 수를 반영하여 준다.
최종적으로 (n - 1, n - 1)칸의 경로의 수를 출력하여 준다.
 

---

❏ 삽질 기록

❍ Issue #1

import sys

input = sys.stdin.readline

n = int(input())
arr = [list(map(int, input().split())) for _ in range(n)]

x, y = 0, 0

stack = [(x, y)]
result = 0
while stack:
    x, y = stack.pop()
    cnt = arr[x][y]
    if arr[x][y] == 0:
        result += 1
        continue
    if x + cnt < n:
        stack.append((x + cnt, y))  # 오른쪽

    if y + cnt < n:
        stack.append((x, y + cnt))  # 왼쪽

print(result)

모든 경우의 수를 체크하며 결과 값을 구해보았다. 시간 초과라는 결과 발생