1260번: DFS와 BFS
첫째 줄에 정점의 개수 N(1 ≤ N ≤ 1,000), 간선의 개수 M(1 ≤ M ≤ 10,000), 탐색을 시작할 정점의 번호 V가 주어진다. 다음 M개의 줄에는 간선이 연결하는 두 정점의 번호가 주어진다. 어떤 두 정점 사
www.acmicpc.net
문제 설명
그래프를 DFS로 탐색한 결과와 BFS로 탐색한 결과를 출력하는 프로그램을 작성하시오. 단, 방문할 수 있는 정점이 여러 개인 경우에는 정점 번호가 작은 것을 먼저 방문하고, 더 이상 방문할 수 있는 점이 없는 경우 종료한다. 정점 번호는 1번부터 N번까지이다.
입력)
첫째 줄에 정점의 개수 N(1 ≤ N ≤ 1,000), 간선의 개수 M(1 ≤ M ≤ 10,000), 탐색을 시작할 정점의 번호 V가 주어진다. 다음 M개의 줄에는 간선이 연결하는 두 정점의 번호가 주어진다. 어떤 두 정점 사이에 여러 개의 간선이 있을 수 있다. 입력으로 주어지는 간선은 양방향이다.
출력)
첫째 줄에 DFS를 수행한 결과를, 그 다음 줄에는 BFS를 수행한 결과를 출력한다. V부터 방문된 점을 순서대로 출력하면 된다.
예제)

❕ 문제 풀이
저번에는 고정적인 크기의 배열로 DFS 문제를 풀었는데, 이번 풀이에서는 가변 배열을 사용해주었다.
DFS의 경우,
1. 시작 노드를 먼저 방문 처리를 해준다.
2. 해당 노드와 연결되어 있는 다른 노드를 방문한 적이 있는지 확인한다.
3. 방문한 적이 없다면, 탐색(재귀)
BFS의 경우,
1. 큐에 시작노드를 먼저 담아주고, 방문 처리를 해준다.
2. 큐에서 노드를 하나씩 꺼내어, 해당 노드에 연결되어 있는 노드를 방문한 적이 있는지 확인한다.
3. 방문한 적이 없다면, 큐에 담고 방문한다.
입력
arr = new ArrayList[n];
for (int i = 0; i < n; i++) {
arr[i] = new ArrayList<>();
}
visited = new boolean[n];
for (int i = 0; i < m; i++) {
st = new StringTokenizer(br.readLine(), " ");
int x = Integer.parseInt(st.nextToken());
int y = Integer.parseInt(st.nextToken());
arr[x - 1].add(y - 1);
arr[y - 1].add(x - 1);
}
for (int i = 0; i < n; i++) {
arr[i].sort(Comparator.naturalOrder());
}입력받은 노드의 번호에 해당하는 인덱스에 연결되는 노드의 번호를 담아주어, 서로를 연결시켜주었다.
또한, 문제에서 번호가 작은 것부터 방문해야한다고 하여 해당 노드에 연결된 노드 번호를 오름차순으로 정렬해준다.

❕ DFS
1. 시작 노드를 먼저 방문 처리를 해준다.
2. 해당 노드와 연결되어 있는 다른 노드를 방문한 적이 있는지 확인한다.
3. 방문한 적이 없다면, 탐색(재귀)
private static void dfs(int v) throws IOException {
visited[v] = true;
bw.write(v + 1 + " ");
for (int i : arr[v]) {
if (!visited[i]) {
dfs(i);
}
}
}
❕ BFS
1. 큐에 시작노드를 먼저 담아주고, 방문 처리를 해준다.
2. 큐에서 노드를 하나씩 꺼내어, 해당 노드에 연결되어 있는 노드를 방문한 적이 있는지 확인한다.
3. 방문한 적이 없다면, 큐에 담고 방문한다.
private static void bfs(int v) throws IOException {
Queue<Integer> queue = new LinkedList<>();
queue.add(v);
visited[v] = true;
while (!queue.isEmpty()) {
v = queue.remove(); // 맨 앞 원소 삭제 & 반환
bw.write(v + 1 + " ");
for (int i : arr[v]) {
if (!visited[i]) {
queue.add(i);
visited[i] = true;
}
}
}
}
✅ [ CODE ]
import java.io.*;
import java.util.*;
public class Main {
static int n, m, v;
static boolean[] visited;
static ArrayList<Integer>[] arr;
static BufferedWriter bw;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
bw = new BufferedWriter(new OutputStreamWriter(System.out));
StringTokenizer st = new StringTokenizer(br.readLine(), " ");
n = Integer.parseInt(st.nextToken());
m = Integer.parseInt(st.nextToken());
v = Integer.parseInt(st.nextToken());
arr = new ArrayList[n];
for (int i = 0; i < n; i++) {
arr[i] = new ArrayList<>();
}
visited = new boolean[n];
for (int i = 0; i < m; i++) {
st = new StringTokenizer(br.readLine(), " ");
int x = Integer.parseInt(st.nextToken());
int y = Integer.parseInt(st.nextToken());
arr[x - 1].add(y - 1);
arr[y - 1].add(x - 1);
}
for (int i = 0; i < n; i++) {
arr[i].sort(Comparator.naturalOrder());
}
dfs(v - 1);
bw.write("\n");
visited = new boolean[n];
bfs(v - 1);
bw.flush();
br.close();
bw.close();
}
private static void bfs(int v) throws IOException {
Queue<Integer> queue = new LinkedList<>();
queue.add(v);
visited[v] = true;
while (!queue.isEmpty()) {
v = queue.remove(); // 맨 앞 원소 삭제 & 반환
bw.write(v + 1 + " ");
for (int i : arr[v]) {
if (!visited[i]) {
queue.add(i);
visited[i] = true;
}
}
}
}
private static void dfs(int v) throws IOException {
visited[v] = true;
bw.write(v + 1 + " ");
for (int i : arr[v]) {
if (!visited[i]) {
dfs(i);
}
}
}
}추가적으로 간선의 연결을 직접적으로 표현할 수 있도록 입력을 받아서 문제 풀이를 해보았다.
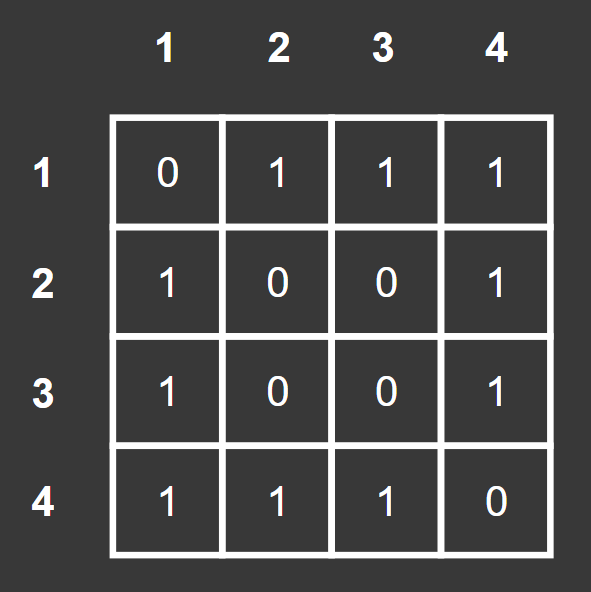
첫 번째 풀이에서는 각 노드에 연결된 노드 번호를 직접적으로 넣어주었는데, 이번에는 고정적인 배열을 통해 인덱스를 노드 번호로 하여 1이면, 간선이 존재하여 연결되었음을 표현해주었다.
풀이는 비슷하나 조금 다른 부분은,
for (int i = 0; i < n; i++) {
if (graph[v][i] == 1 && !visited[i]) {
dfs(i);
}
}이런 식으로 간선이 존재하는지를 추가적으로 조건문에 담아주었다.
✅ [ CODE ]
import java.io.*;
import java.util.LinkedList;
import java.util.Queue;
import java.util.StringTokenizer;
public class Main2 {
static int n, m, v;
static int[][] graph;
static boolean[] visited;
static BufferedWriter bw;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
bw = new BufferedWriter(new OutputStreamWriter(System.out));
StringTokenizer st = new StringTokenizer(br.readLine(), " ");
n = Integer.parseInt(st.nextToken());
m = Integer.parseInt(st.nextToken());
v = Integer.parseInt(st.nextToken());
visited = new boolean[n];
graph = new int[n][n];
for (int i = 0; i < m; i++) {
st = new StringTokenizer(br.readLine(), " ");
int x = Integer.parseInt(st.nextToken());
int y = Integer.parseInt(st.nextToken());
graph[x - 1][y - 1] = 1;
graph[y - 1][x - 1] = 1;
}
dfs(v - 1);
bw.write("\n");
visited = new boolean[n];
bfs(v - 1);
bw.flush();
br.close();
bw.close();
}
private static void bfs(int v) throws IOException {
Queue<Integer> queue = new LinkedList<>();
queue.add(v);
visited[v] = true;
while (!queue.isEmpty()) {
v = queue.remove();
bw.write(v + 1 + " ");
for (int i = 0; i < n; i++) {
if (graph[v][i] == 1 && !visited[i]) {
queue.add(i);
visited[i] = true;
}
}
}
}
private static void dfs(int v) throws IOException {
visited[v] = true;
bw.write(v + 1 + " ");
for (int i = 0; i < n; i++) {
if (graph[v][i] == 1 && !visited[i]) {
dfs(i);
}
}
}
}