[Algorithm/Python] 퀵 정렬(Quick Sort)이란? || Sort

📌 퀵 정렬(Quick Sort)

퀵 정렬(Quick Sort)이란 기준 데이터인 피벗(pivot)을 정하고, 피벗보다 큰 데이터와 작은 데이터의 위치를 변경하는 정렬 방식이다.
피벗이 설정되어 리스트가 분할되는 방법에 따라 여러 퀵 정렬이 구분된다고 하는데, 호어 분할 방식에 따른 코드 구현을 진행해보았다.
 
호어 분할 방식에는 리스트에서 첫 번째 데이터를 피벗으로 설정한다는 규칙이 있다.
1️⃣ 리스트의 첫 번째 데이터를 피벗으로 설정한 후, 리스트의 왼쪽에서 오른쪽으로 이동하며 피벗보다 큰 데이터를 찾는다. 또한, 리스트의 오른쪽에서 왼쪽으로 이동하며 피벗보다 작은 데이터를 찾는다.
2️⃣ 큰 데이터와 작은 데이터의 위치를 서로 바꾼다.
3️⃣ 이와 같은 과정을 반복하되, 큰 데이터의 위치와 작은 데이터의 위치가 서로 엇갈린다면, 피벗과 작은 데이터의 위치를 바꾼다.
 
그러면, 피벗을 기준으로 리스트의 왼쪽 부분과 오른쪽 부분을 다시 위와 같은 과정을 반복하도록 한다. 분할된 리스트의 크기가 1이 된다면, 퀵 정렬을 마친다.
위와 같은 과정을 글로만 보면, 잘 와닿지 않아 그림과 함께 이해하는 것이 큰 도움이 된다.
 

1. 파란 박스인 리스트의 첫 번째 데이터, 5가 피벗이 된다.
 

2. 리스트의 왼쪽부터 피벗인 5보다 큰 데이터인 7을 찾고, 리스트의 오른쪽부터 피벗인 5보다 작은 데이터인 4를 찾는다.
 

3. 둘의 데이터 위치를 변환한 후, 같은 과정을 반복한다. 그러나, 큰 데이터와 작은 데이터의 위치가 어긋나는 순간이라면, 작은 데이터와 피벗의 위치를 변환한다.
 

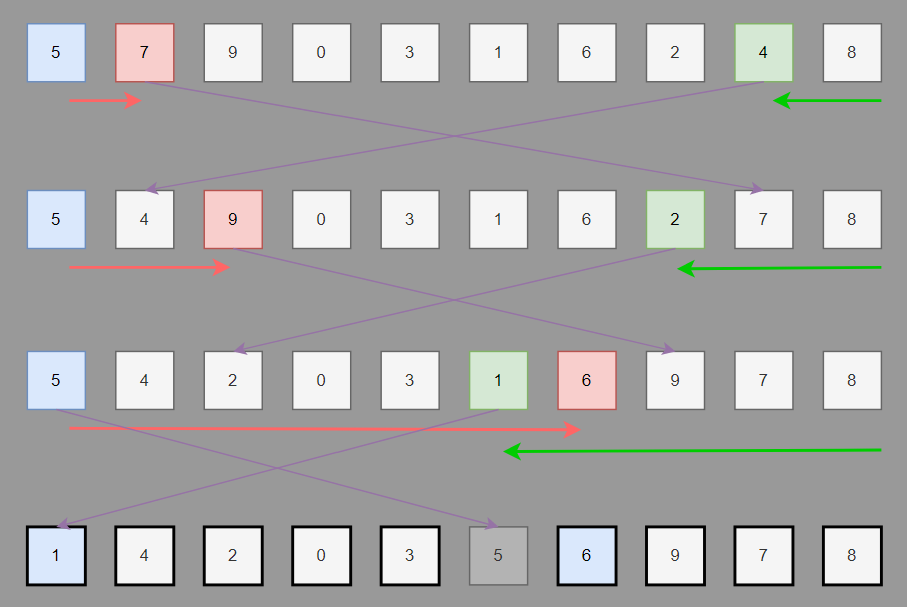
4. 기존의 피벗이었던 5를 기준으로 좌측, 우측으로 리스트가 분할된다. 각 리스트의 첫 번째 데이터가 피벗이 되며, 1 ~ 3과 같은 과정이 반복되며 정렬이 이루어 진다.
 

✅ [ CODE ]

arr = [7, 5, 9, 0, 3, 1, 6, 2, 4, 8]

def quick(arr, start, end):
    if end - start < 1:
        return
    pivot = arr[start]
    i, j = 0, 0
    while True:
        for x in range(start + 1, end + 1):
            if pivot < arr[x]:
                i = x
                break
        for x in range(end, start, -1):
            if pivot > arr[x]:
                j = x
                break
        if i != 0 and j != 0:
            if i > j:
                arr[start], arr[j] = arr[j], arr[start]
                break
            arr[i], arr[j] = arr[j], arr[i]
        elif i == 0:
            arr[start:end] = arr[start+1:end+1]
            arr[end] = pivot
            j = end - 1
            break
        elif j == 0:
            j = start
            break
    quick(arr, start, j)
    quick(arr, j + 1, end)

quick(arr, 0, len(arr) - 1)
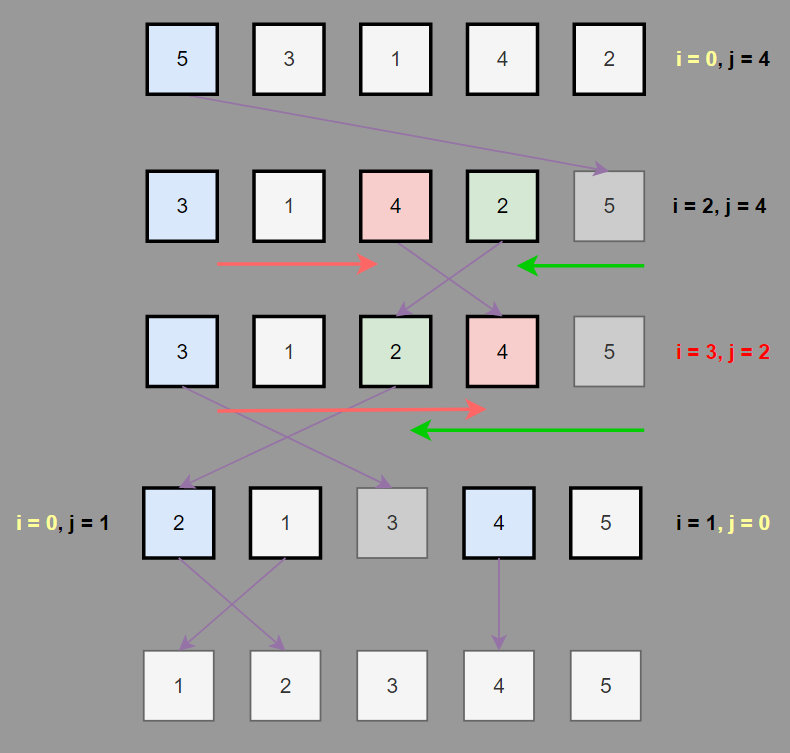
print(arr)

1. i는 큰 데이터, j는 작은 데이터의 인덱스를 의미한다. 피벗과 비교하는 for문을 거쳐 각각 알맞은 데이터의 값을 구해온다.
2. i와 j가 0이 아니며, i와 j가 엇갈리지 않는다면(i < j), i와 j의 데이터 위치를 변환한다.
    a. 만약 엇갈린다면 (i > j), 피벗과 작은 데이터의 위치를 변환한다.
3. i가 0이라면, 피벗보다 큰 데이터가 존재하지 않음을 의미하므로, 리스트의 맨 뒤로 이동한다.
4. j가 0이라면, 피벗보다 작은 데이터가 존재하지 않음을 의미하므로, 리스트에 변화가 없다.

 
 

✅ [ CODE ]

while문에 조건을 적용시켜 이전의 훨씬 지저분해 보였던 코드를 깔끔하게 바꾸어줄 수 있다.

arr = [7, 5, 9, 0, 3, 1, 6, 2, 4, 8]

def quick(arr, start, end):
    if start >= end:
        return
    pivot = start
    left = start + 1
    right = end
    while left <= right:
        while left <= right and arr[left] <= arr[pivot]:
            left += 1

        while left <= right and arr[right] >= arr[pivot]:
            right -= 1

        if left > right:
            arr[right], arr[pivot] = arr[pivot], arr[right]
        else:
            arr[left], arr[right] = arr[right], arr[left]

    quick(arr, start, right - 1)
    quick(arr, right + 1, end)

quick(arr, 0, len(arr) - 1)
print(arr)

1번의 코드를 함께 비교해보자면, 1번 코드에서는 피벗이 맨 앞을 그대로 유지해야 하거나, 맨 뒤로 변환해야할 때, i와 j의 값이 0인지를 체킹해주어야 했다.
그러나, 위의 코드의 경우 left > right의 조건문 하나만으로 1번 코드에서의 번거로움을 줄일 수 있었다. 피벗이 맨 앞을 그대로 유지해야 하는 경우에는 left > right의 조건에 적합하지 않으므로, 그대로 while문이 자동 종료된다. 또한, 피벗이 맨 뒤로 이동해야 하는 경우는, 즉시 맨 뒤로 이동하지 않고 그저 작은 데이터(j)와의 변환만으로 추후에 맨 뒤로 정렬되며 위치할 수 있도록 구동된다.
 

✅ [ CODE ]

arr = [7, 5, 9, 0, 3, 1, 6, 2, 4, 8]

def quick(arr):
    print(arr)
    if len(arr) <= 1:
        return arr
    
    pivot = arr[0]
    tail = arr[1:]

    left_side = [x for x in tail if x <= pivot]
    right_side = [x for x in tail if x > pivot]

    return quick(left_side) + [pivot] + quick(right_side)

print(quick(arr))

피벗을 제외한 모든 리스트를 피벗과 비교하여 피벗보다 작은 부분과 큰 부분으로 리스트를 분할한다. 이를 반복하여 최종적으로 정렬된 리스트를 반환하게 된다.
이는, 모든 원소를 피벗과 계속 비교하기 때문에 비효율적인 편이지만, 퀵 정렬을 기억하기 편리한 장점이 있다.
 

📌 시간 복잡도

퀵 정렬의 평균 시간 복잡도는 O(NlogN)이다. 이름처럼 다른 선택 정렬과 삽입 정렬의 최악의 시간 복잡도가 O(N^2)인 것을 고려하면 시간이 빠르다.
그렇지만, 리스트가 어느정도 정렬이 되어있는 경우에는 매우 느리게 동작한다.
삽입 정렬의 경우, 어느 정도 정렬이 되어있는 리스트라면 빠르게 동작하지만, 퀵 정렬은 이와 반대된다는 점이 특징이다.
 
출처) 이것이 코딩테스트다 with Python