[Algorithm/Python] 삽입 정렬(Insertion Sort)이란? || Sort

📌 삽입 정렬(Insertion Sort)

삽입 정렬

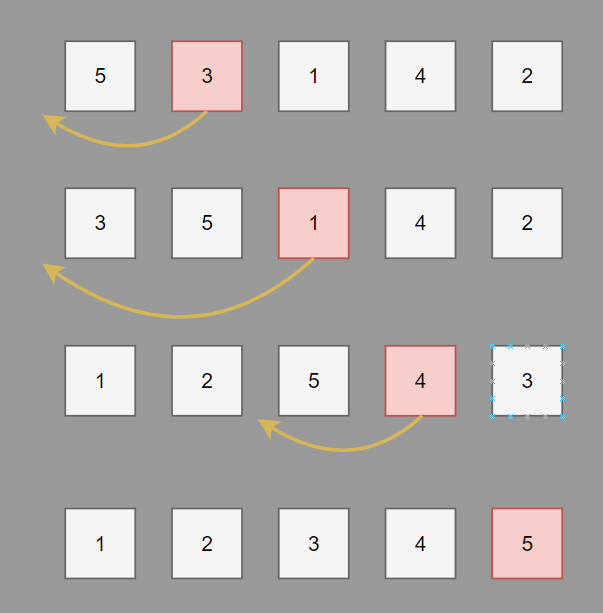
삽입 정렬은 순차적으로 데이터를 확인하며, 적절한 위치에 삽입해주는 정렬 방식이다.
그림을 보면, 인덱스 1번째 수부터 시작하여 차례대로 각자 적절한 위치에 삽입해주는 것을 확인해볼 수 있다.
 
적절한 위치인 곳을 찾는 방법은, 빨간 박스로된 수를 기준으로 왼쪽으로 한 칸씩 이동하며 값을 비교한다.
빨간 박스의 수보다 작은 수를 만나게 되는 순간, 바로 그 위치에 삽입해주면 된다.
 

✅ [ CODE ]

arr = [7, 5, 9, 0, 3, 1, 6, 2, 4, 8]

for i in range(1, len(arr)):
    idx = i
    for j in range(i, -1, -1):
        if arr[i] < arr[j]:
            idx = j
    val = arr[i]
    arr[idx + 1 : i + 1] = arr[idx : i]
    arr[idx] = val
            
print(arr)

예를 들어, [5, 7, 9, 0]에서 0이 들어갈 적절한 위치를 찾는다고 해보자면,
5, 7, 9와 비교하며, 0보다 클 때마다 해당 인덱스를 기억해둔다. 
그 후, [5, 7, 9, 0]에서 0번째 인덱스에 수를 넣기 위해 5, 7, 9를 오른쪽으로 한 칸 이동시킨다.
[5, 5, 7, 9]처럼 이동 후 0번째 인덱스에 0을 넣어 정렬을 마친다. [0, 5, 7, 9]
 

✅ [ CODE ]

arr = [7, 5, 9, 0, 3, 1, 6, 2, 4, 8]

for i in range(1, len(arr)):
    for j in range(i, 0, -1):
        if arr[j] < arr[j - 1]:
            arr[j], arr[j - 1] = arr[j - 1], arr[j]
        else:
            break
print(arr)

또다시, [5, 7, 9, 0]에서 0이 들어갈 적절한 위치를 찾는다고 해보자면,
5, 7, 9와 비교하며, 0보다 클 때마다, 위치를 스와핑한다.
[ 5, 7, 0, 9 ] → [ 5, 0, 7, 9 ] → [ 0, 5, 7, 9 ]
 
선택 정렬과 마찬가지로 이중 for문으로 시간 복잡도는 $O(N^2)$이다.
그러나 삽입 정렬은 이미 정렬이 어느정도 진행되어 있는 경우, 훨씬 빠르게 동작하므로, 최선의 경우 $O(N)$의 시간복잡도를 가진다.
 
참고) 이것이 코딩 테스트다 with 파이썬