https://www.acmicpc.net/problem/15686
15686번: 치킨 배달
크기가 N×N인 도시가 있다. 도시는 1×1크기의 칸으로 나누어져 있다. 도시의 각 칸은 빈 칸, 치킨집, 집 중 하나이다. 도시의 칸은 (r, c)와 같은 형태로 나타내고, r행 c열 또는 위에서부터 r번째 칸
www.acmicpc.net
문제
크기가 N×N인 도시가 있다. 도시는 1 ×1 크기의 칸으로 나누어져 있다. 도시의 각 칸은 빈칸, 치킨집, 집 중 하나이다. 도시의 칸은 (r, c)와 같은 형태로 나타내고, r행 c열 또는 위에서부터 r번째 칸, 왼쪽에서부터 c번째 칸을 의미한다. r과 c는 1부터 시작한다.
이 도시에 사는 사람들은 치킨을 매우 좋아한다. 따라서, 사람들은 "치킨 거리"라는 말을 주로 사용한다. 치킨 거리는 집과 가장 가까운 치킨집 사이의 거리이다. 즉, 치킨 거리는 집을 기준으로 정해지며, 각각의 집은 치킨 거리를 가지고 있다. 도시의 치킨 거리는 모든 집의 치킨 거리의 합이다.
임의의 두 칸 (r1, c1)과 (r2, c2) 사이의 거리는 |r1-r2| + |c1-c2|로 구한다.
예를 들어, 아래와 같은 지도를 갖는 도시를 살펴보자.
0 2 0 1 0
1 0 1 0 0
0 0 0 0 0
0 0 0 1 1
0 0 0 1 2
0은 빈 칸, 1은 집, 2는 치킨집이다.
(2, 1)에 있는 집과 (1, 2)에 있는 치킨집과의 거리는 |2-1| + |1-2| = 2, (5, 5)에 있는 치킨집과의 거리는 |2-5| + |1-5| = 7이다. 따라서, (2, 1)에 있는 집의 치킨 거리는 2이다.
(5, 4)에 있는 집과 (1, 2)에 있는 치킨집과의 거리는 |5-1| + |4-2| = 6, (5, 5)에 있는 치킨집과의 거리는 |5-5| + |4-5| = 1이다. 따라서, (5, 4)에 있는 집의 치킨 거리는 1이다.
이 도시에 있는 치킨집은 모두 같은 프랜차이즈이다. 프랜차이즈 본사에서는 수익을 증가시키기 위해 일부 치킨집을 폐업시키려고 한다. 오랜 연구 끝에 이 도시에서 가장 수익을 많이 낼 수 있는 치킨집의 개수는 최대 M 개라는 사실을 알아내었다.
도시에 있는 치킨집 중에서 최대 M개를 고르고, 나머지 치킨집은 모두 폐업시켜야 한다. 어떻게 고르면, 도시의 치킨 거리가 가장 작게 될지 구하는 프로그램을 작성하시오.
입력/출력
첫째 줄에 N(2 ≤ N ≤ 50)과 M(1 ≤ M ≤ 13)이 주어진다.
둘째 줄부터 N개의 줄에는 도시의 정보가 주어진다.
도시의 정보는 0, 1, 2로 이루어져 있고, 0은 빈 칸, 1은 집, 2는 치킨집을 의미한다. 집의 개수는 2N개를 넘지 않으며, 적어도 1개는 존재한다. 치킨집의 개수는 M보다 크거나 같고, 13보다 작거나 같다.
---
첫째 줄에 폐업시키지 않을 치킨집을 최대 M개를 골랐을 때, 도시의 치킨 거리의 최솟값을 출력한다.
문제 풀이
예제 1 도시에서는 집(1)과 치킨집(2)이 다음과 같이 구성되어있다.
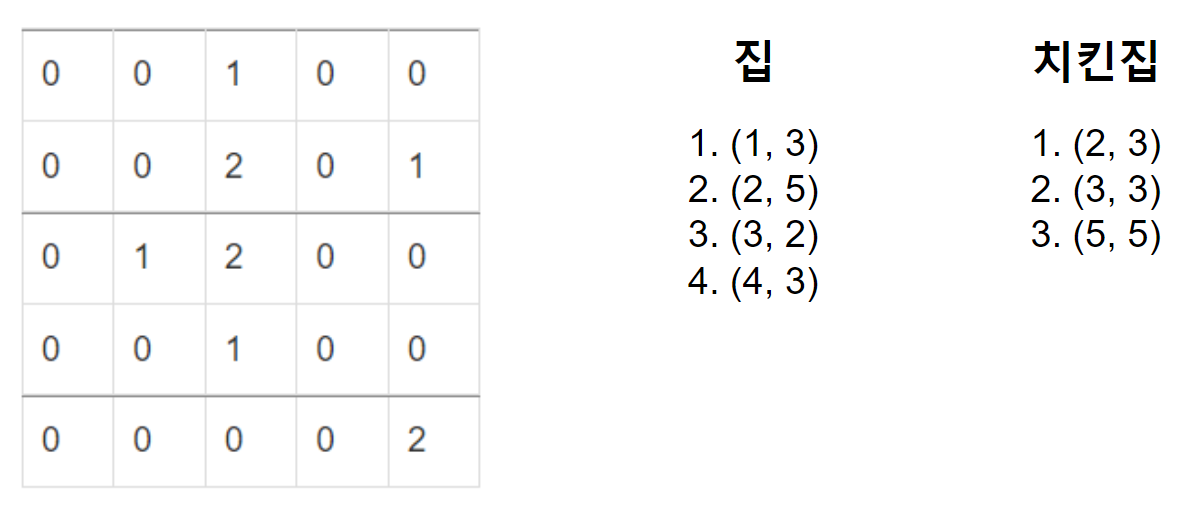
집 (1, 3) 에서 각 치킨집까지의 거리는 1, 2, 6이므로 치킨 거리는 1이다.
집 (2, 5)는 2, (3, 2)는 1, (4, 3)는 1이 각각의 치킨 거리이다.
도시의 치킨 거리는 1 + 2 + 1 + 1 = 5이다.
1. 도시에서 집과 치킨집 위치 리스트를 뽑아낸다.
2. 기존 치킨집에서 M개의 치킨집을 고른다.
3. 골라진 여러 치킨집에서 도시의 치킨 거리를 구한다.
4. 도시의 치킨 거리의 최솟값을 구한다.
1. 집과 치킨집의 위치
# 집과 치킨집 구하기
for i in range(n):
for j in range(n):
if city[i][j] == 1:
home.append((i + 1, j + 1))
elif city[i][j] == 2:
chicken.append((i + 1, j + 1))N x N 크기의 도시를 전체 스캔해나가며 집(1)과 치킨집(2)의 위치를 튜플을 이용하여 리스트에 저장해주었다.
2. M개의 치킨집 고르기
입력된 N개의 치킨집에서 폐업되지 않을 M개의 치킨집을 골라야 한다. 중복 없이, 순서를 고려하지 않고 뽑는 경우이므로 조합을 이용해준다.
파이썬에서 조합을 이용해주는 방법은 itertools 라이브러리를 이용한다. 반복되는 데이터를 처리하는 기능을 제공해주는 라이브러리로, 순열(permutations)과 조합(combinations) 기능을 제공한다.
from itertools import combinations
# 최대 m개 만큼 치킨집 조합
chicken_list = list(combinations(chicken, m))nCm, 5C2라면 10개의 조합으로 치킨집 리스트를 구해준다.
3. 도시의 치킨 거리 구하기
조합을 통해 구해진 치킨집들을 이용해, 집에서 각 치킨집과의 거리를 구하고, 그중 가장 최솟값인 치킨 거리를 구한다.
그 후 총 치킨 거리의 합인 도시의 치킨 거리를 구한다.
# 도시의 치킨 거리
def find_dist(home, chicken):
city_dist = 0
for i in home:
min_val = float('inf') # 임의의 가장 큰 수
for j in chicken:
# dist = abs(i[0] - j[0]) + abs(i[1] - j[1])
# if min_val > dist:
# min_val = dist
min_val = min(min_val, abs(i[0] - j[0]) + abs(i[1] - j[1]))
city_dist += min_val
return city_dist
4. 최종 도시의 치킨 거리
각 조합에 따라 구해진 도시의 치킨 거리 중 가장 최솟값을 출력한다.!
min_dist = float('inf')
for i in chicken_list:
# dist = find_dist(home, i)
# if min_dist > dist:
# min_dist = dist
min_dist = min(min_dist, find_dist(home, i))
# 가장 작은 도시의 치킨 거리 출력
print(min_dist)✅[ CODE ]
from itertools import combinations
# 도시의 치킨 거리
def find_dist(home, chicken):
city_dist = 0
for i in home:
min_val = float('inf') # 임의의 가장 큰 수
for j in chicken:
# dist = abs(i[0] - j[0]) + abs(i[1] - j[1])
# if min_val > dist:
# min_val = dist
min_val = min(min_val, abs(i[0] - j[0]) + abs(i[1] - j[1]))
city_dist += min_val
return city_dist
n, m = map(int, input().split())
city = []
for _ in range(n):
city.append(list(map(int, input().split())))
home = []
chicken = []
# 집과 치킨집 구하기
for i in range(n):
for j in range(n):
if city[i][j] == 1:
home.append((i + 1, j + 1))
elif city[i][j] == 2:
chicken.append((i + 1, j + 1))
# 최대 m개 만큼 치킨집 조합
chicken_list = list(combinations(chicken, m))
min_dist = float('inf')
for i in chicken_list:
# dist = find_dist(home, i)
# if min_dist > dist:
# min_dist = dist
min_dist = min(min_dist, find_dist(home, i))
# 가장 작은 도시의 치킨 거리 출력
print(min_dist)조합을 통해 경우의 수를 모두 구하고, 조합에 맞게 치킨 거리를 모두 구하는 브루트포스 알고리즘을 이용하였다.