[Algorithm/Python] 크루스칼 알고리즘이란? || 최소 신장 트리

들어가며

본 포스팅에서는 신장 트리에 대해 그리고 최소 신장 트리 알고리즘인 크루스칼 알고리즘에 대해 소개합니다.
 

📌 신장 트리란?

신장 트리(Spanning Tree)란 하나의 그래프가 있을 때, 모든 노드를 포함하면서 사이클이 존재하지 않는 부분 그래프를 말합니다.

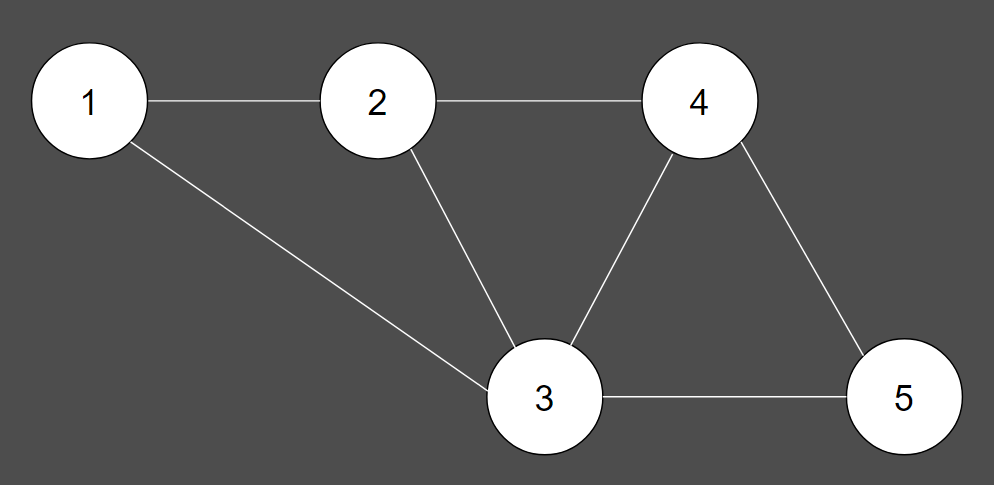
예를 들어 위와 같은 그래프가 존재한다고  할 때, 아래의 경우는 신장 트리인지를 확인해보겠습니다.
 

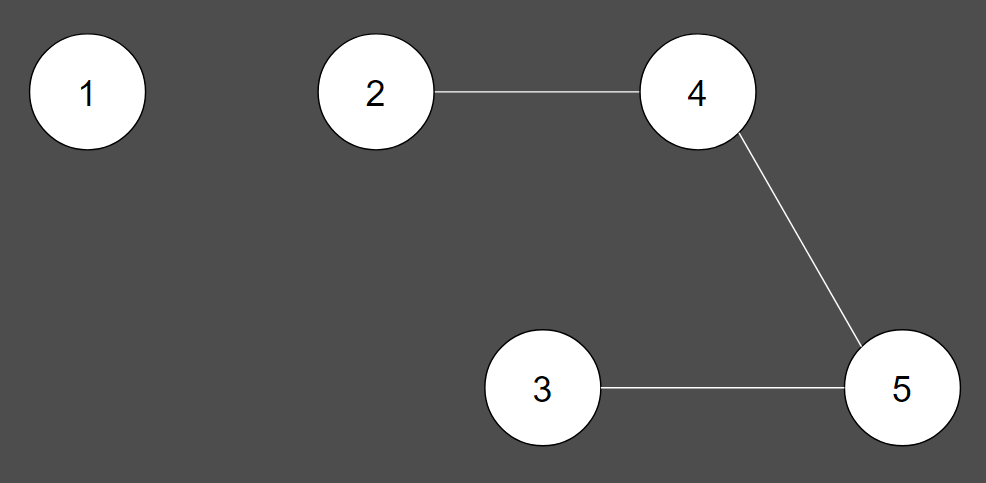
이 그래프는 노드 1을 포함하고 있지 않기 때문에 신장 트리에 해당하지 않습니다.
 

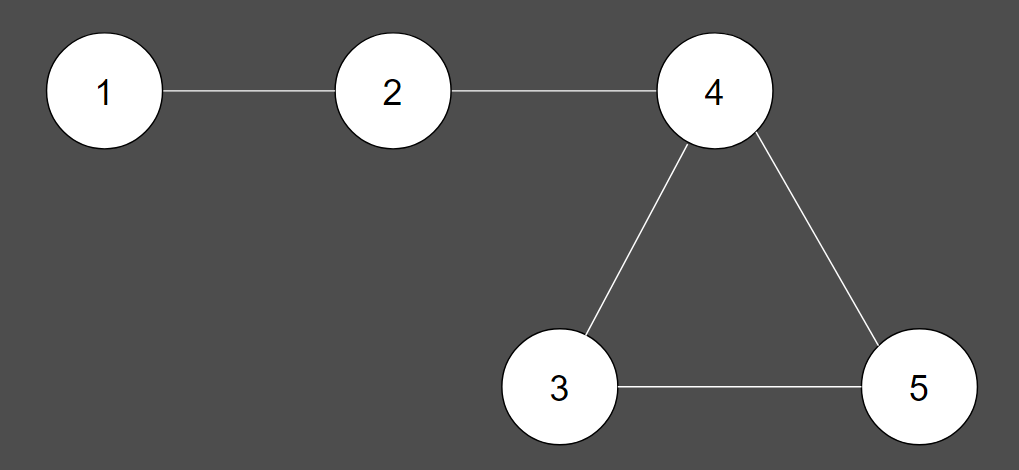
이 그래프는 모든 노드를 포함하고 있지만, 사이클이 존재하므로 신장 트리에 해당하지 않습니다.
 

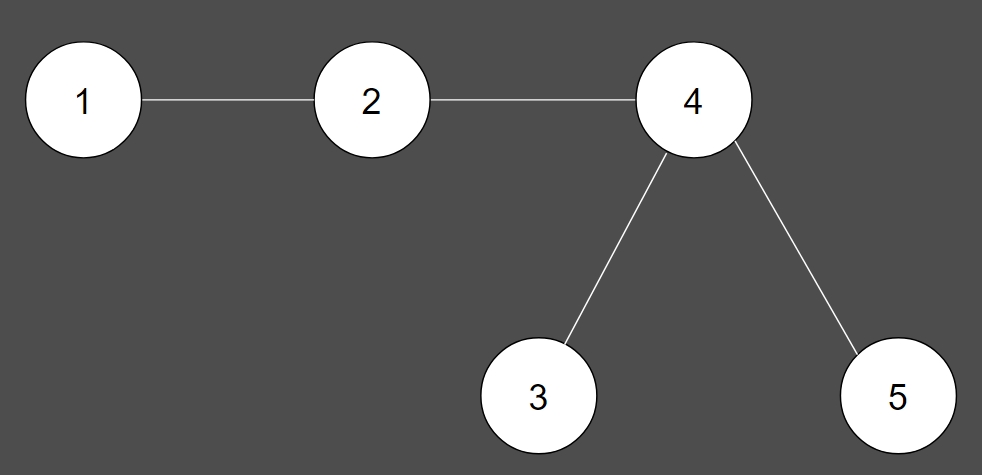
이 그래프는 모든 노드를 포함하고 있으며, 사이클이 존재하지 않으므로 신장 트리에 해당합니다.
 
신장 트리의 노드 개수와 간선의 관계를 보면, 노드의 개수가 5개일 때, 간선의 개수는 4개입니다. 최종적으로 신장 트리에 포함되는 간선의 개수는 "노드의 개수 - 1"라는 점이 특징입니다.
 

📌 크루스칼 알고리즘이란?

최소 비용으로 신장 트리를 찾는 알고리즘인 최소 신장 트리 알고리즘 중에 크루스칼(Kruskal) 알고리즘이 있습니다.
 
1️⃣ 간선의 비용에 따라 오름차순으로 정렬합니다.
2️⃣ 간선이 사이클을 발생시키는지 확인합니다.
- 1 ) 사이클이 발생하지 않는 경우, 최소 신장 트리에 포함시킵니다.
- 2 ) 사이클이 발생하는 경우, 포함시키지 않습니다.
3️⃣ 모든 간선에 대하여 위의 과정을 반복합니다.
 
이처럼 모든 간선에 대해 차례대로 확인하며 최소 신장 트리에 포함하므로 그리디 알고리즘으로 분류됩니다.
 
1. 모든 간선에 따른 비용을 확인한 후 오름차순 정렬을 해줍니다.

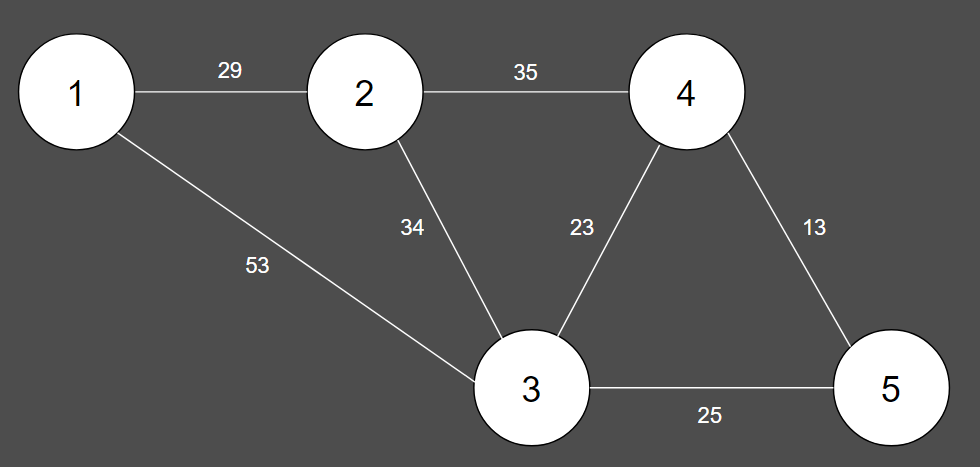
간선	(1, 2)	(1, 3)	(2, 3)	(2, 4)	(3, 4)	(3, 5)	(4, 5)
비용	29	53	34	35	23	25	13

 

간선	(4, 5)	(3, 4)	(3, 5)	(1, 2)	(2, 3)	(2, 4)	(1, 3)
비용	13	23	25	29	34	35	53

 
2. 가장 짧은 간선을 선택하여 union 연산을 수행합니다.

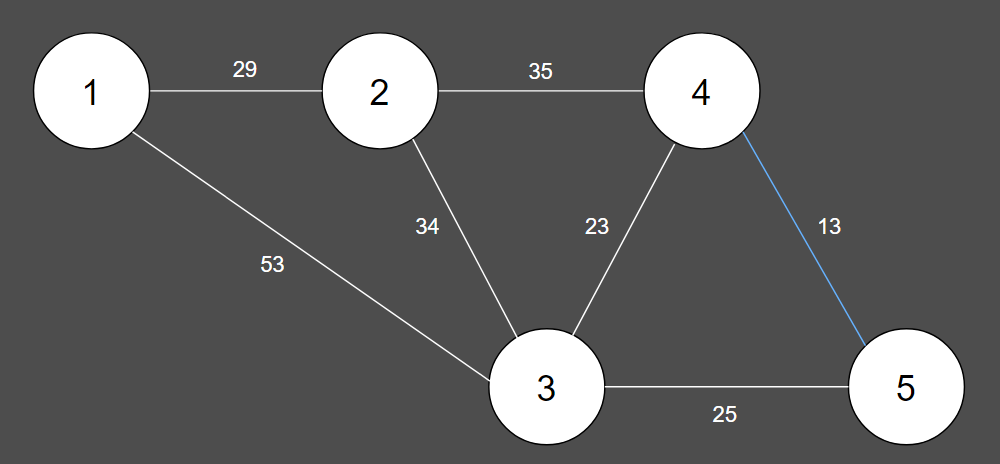
간선	(4, 5)	(3, 4)	(3, 5)	(1, 2)	(2, 3)	(2, 4)	(1, 3)
비용	13	23	25	29	34	35	53

 
3. 그 다음 짧은 간선을 선택하여 union 연산을 수행합니다.

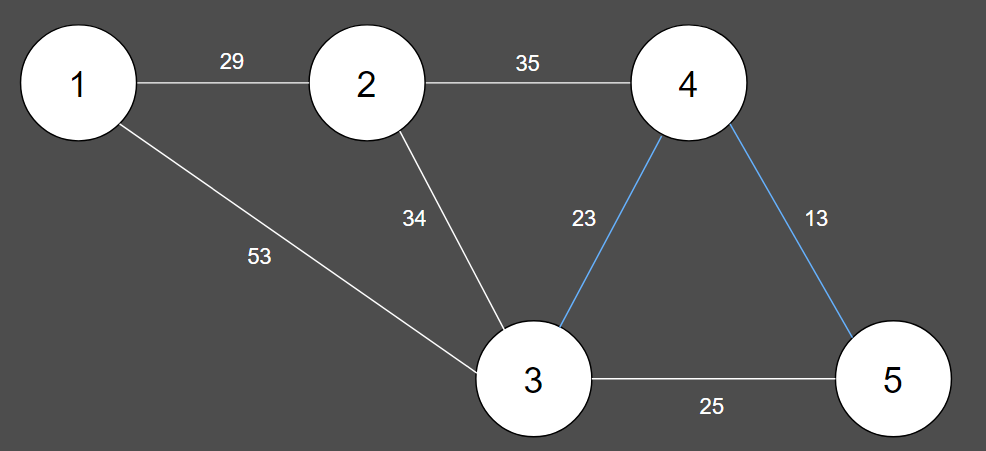
간선	(4, 5)	(3, 4)	(3, 5)	(1, 2)	(2, 3)	(2, 4)	(1, 3)
비용	13	23	25	29	34	35	53

 
 
 
4. 그 다음 짧은 간선은 이미 동일한 집합에 포함되어 있으므로 union 연산이 수행되지 않습니다.

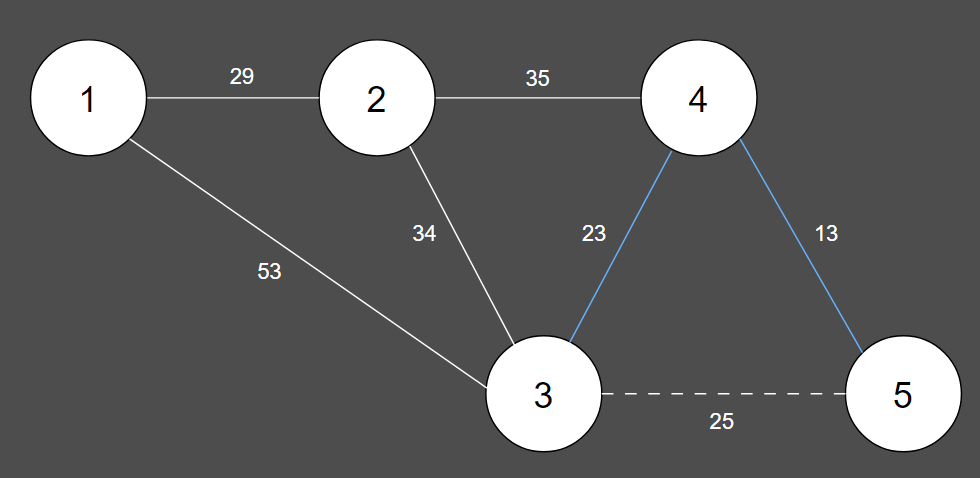
간선	(4, 5)	(3, 4)	(3, 5)	(1, 2)	(2, 3)	(2, 4)	(1, 3)
비용	13	23	25	29	34	35	53

 
5. 그 다음 짧은 간선을 선택하여 union 연산을 수행합니다.

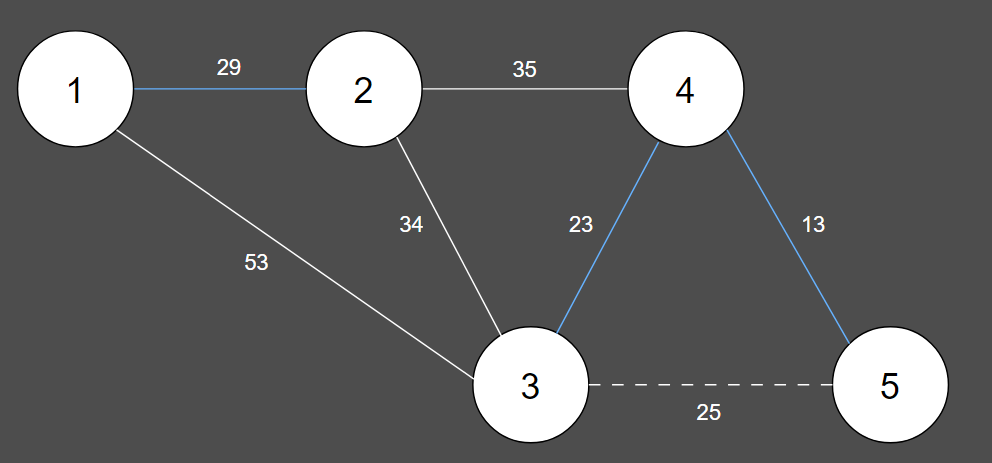
간선	(4, 5)	(3, 4)	(3, 5)	(1, 2)	(2, 3)	(2, 4)	(1, 3)
비용	13	23	25	29	34	35	53

 
6. 그 다음 짧은 간선을 선택하여 union 연산을 수행합니다.

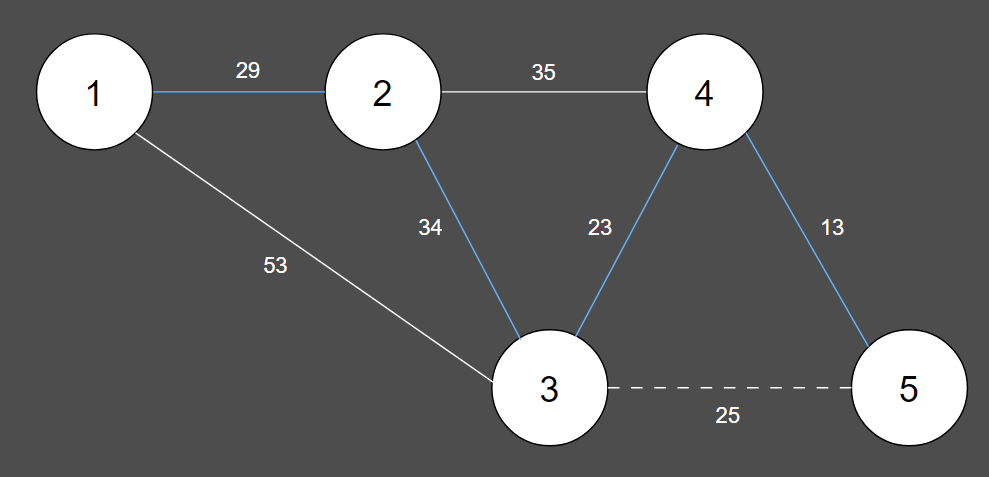
간선	(4, 5)	(3, 4)	(3, 5)	(1, 2)	(2, 3)	(2, 4)	(1, 3)
비용	13	23	25	29	34	35	53

 
7. 그 다음 짧은 간선은 이미 동일한 집합에 포함되어 있으므로 union 연산이 수행되지 않습니다.

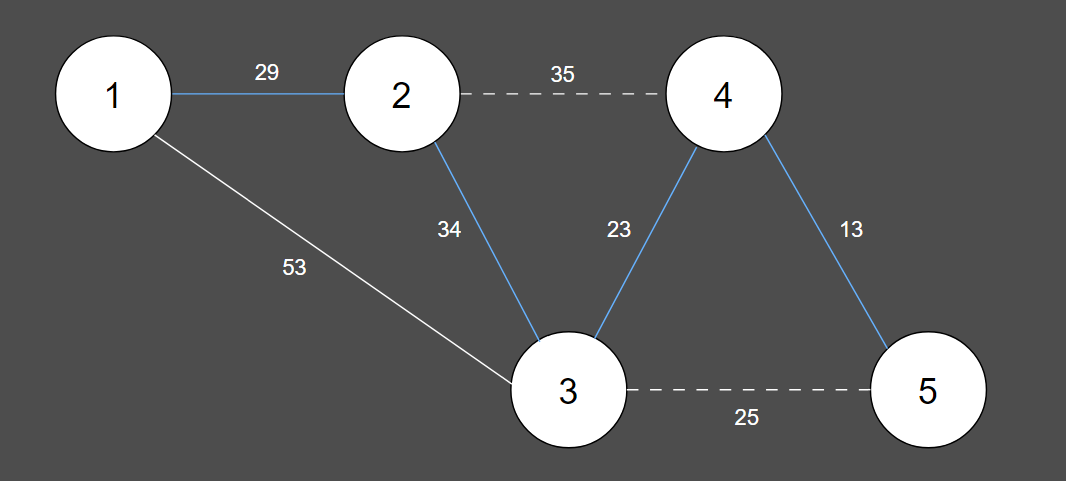
간선	(4, 5)	(3, 4)	(3, 5)	(1, 2)	(2, 3)	(2, 4)	(1, 3)
비용	13	23	25	29	34	35	53

 
8. 그 다음 짧은 간선은 이미 동일한 집합에 포함되어 있으므로 union 연산이 수행되지 않습니다.

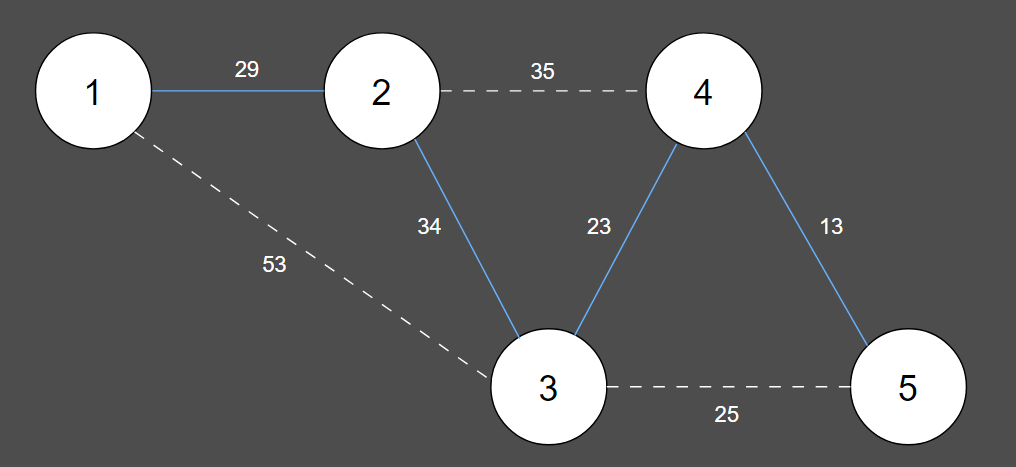
간선	(4, 5)	(3, 4)	(3, 5)	(1, 2)	(2, 3)	(2, 4)	(1, 3)
비용	13	23	25	29	34	35	53

 

✅ [ CODE ]

import sys


def find_parent(parent, a):
    if parent[a] != a:
        parent[a] = find_parent(parent, parent[a])
    return parent[a]


def union_parent(parent, a, b):
    a = find_parent(parent, a)
    b = find_parent(parent, b)
    if a < b:
        parent[b] = a
    else:
        parent[a] = b


input = sys.stdin.readline
v, e = map(int, input().split())
parent = [0] * (v + 1)

for i in range(1, v + 1):
    parent[i] = i

edges = []
result = 0

for _ in range(e):
    a, b, cost = map(int, input().split())
    edges.append((a, b, cost))

edges.sort(key=lambda x: x[2])

for a, b, cost in edges:
    if find_parent(parent, a) != find_parent(parent, b):
        union_parent(parent, a, b)
        result += cost

print(result)

 

☑️ 시간 복잡도

크루스칼 알고리즘은 간선의 개수가 E개일 때, $O(ElogE)$의 시간 복잡도를 가집니다. 정렬 작업이 가장 오래 걸리는 작업이며, 서로소 집합 알고리즘보다 크므로 정렬 시간 복잡도인 $O(ElogE)$가 됩니다.
 

---

포스팅 내용에 오류 및 문제가 있는 경우, 댓글로 알려주시면 감사하겠습니다.
파이팅.......................!